반도체 공급 부족

 2020년 후반부터 반도체 부족은 심각해지고 2021년이 지났지만 반도체 공급 부족이라는 문제의 해결은 멀어져간다.  이것은 2020년 전반부터 시작된 COVID-19(신형 코로나바이러스 감염증)으로 시작되었는데, 판데믹이라는 세계적인 대 유행은 경기하강으로 수요가 줄 것이라는 우려와는 반대로 반도체 수요를 크게 증가 시키는 방향으로 나아갔다. 

 코로나 바이러스는 연속적으로 돌연변이로 파생되었다. 초기에는 위험성이 강했지만, 점차 변이가 되면서 전파되는 감염력이 강한 오미크론이 주가 되었고, 2022년 3월 시점에서는, 감염성은 아주 크지만, 위험성은 약하기 때문에 제한적인 부분부터 경제활동의 제한을 완화하고, 백신접종의 보급을 병행하면서 위험성에 대비하고, 그래서 중증화를 막는 대책이 선진국의 주류가 되었다. 

경제활동의 재개는 반도체 수요의 추가 확대를 의미한다. 반도체 부족이 완화되는 것은 2024년이 된다는 것이 반도체 업계에서는 거의 공통의 전망이다.

반도체 부족의 완화를 위한 큰 움직임이 생산규모의 증강이다. 장래의 생산능력은 현재의 설비투자금액에 크게 좌우된다. 한 연차 설비투자는 대략 2년 후에 실제 양산공장, 즉 생산능력이 증가하여 현실화한다.

시장조사회사인 IC Insights가 2022년 3월 1일에 발표한 조사 결과에 따르면 2022년 반도체 설비 투자액은 전년 대비 24% 증가한 1,904억 달러에 달하는 모양이다. 반도체 설비투자액은 2020년 전년 대비 10% 증가해 과거 최고를 경신했다. 이어 2021년은 전년 대비 36% 증가한 1,539억 달러로 급증해 과거 최고의 갱신을 이어갔다. 이대로 3년 연속으로 설비투자액은 과거 최고를 갱신하게 된다.

2022년 초대형 설비투자는 2024년에는 생산능력의 대폭 증가가 되어 현실화될 것으로 보인다. 이것은 판데믹 유행 초기에 우려했던 수요 감소가, 2024년에 나타날 것으로 보이며, 이 예측이 현실이 되면 반도체 공급과잉과 가격이 붕괴한다. 반도체 업계는 과거에도 같은 것을 경험하고 있기 때문에 수급 밸런스를 항상 주의깊게 보고 있다. 수급이 크게 완화될 것 같은 경우는 2023년 후반~2024년 전반에 제조 장치의 납품을 앞두는 움직임이 있을 것이다.

Integer Quantization for Deep Learning Inference

 Nvidia에서 발간한 Integer Quantization for Deep Learning Inference이다. 2020년 4월에 공개되었으며, Low Bit 양자화에 대한 개념을 소개하고 있다. 있 

Uniform vs Non-Uniform

양자화를 진행하는 방법에는 큰 범주에서 2가지가 있다. 먼저 균일 양자화(Uniform) 방법이다. 이는 Floating Point로 되어있는 Input이나 가중치를 정수형태 또는 고정소수점 형태로 변환하여 연산하는 형태이다. 변환 이후의 값이 가지는 표현범위를 보면 균일한 간격으로 구성이 되어있다. 예를 들어 8-Bit 데이터 타입이라면 -128 ~ 127까지 표현 범위를 가지고 있으며 간격은 1씩 떨어져있다.

 

비균일 양자화(Non-Uniform)은 일반적으로 Code Book을 사용하여 맵핑을 하는 방식을 택한다. 예를들어 가중치가 [[0.1, 0.5, -1.2], [-2.1, 1.5, 0.1], [-3.1, 2.1, 0.3]] 이라고 하였을때, 음수: 0, 0~1:1, 1이상:2 이렇게 대응되는 코드북을 만드는 개념이다. 사용자가 정해놓은 Rule을 적용해서 이 코드북을 만들기 때문에 비균일 양자화 방법이라고 한다. 논문에서는 균일 양자화에 대해서만 초점을 맞춰 진행한다.

 

 

Affine Transform vs Scale Transform

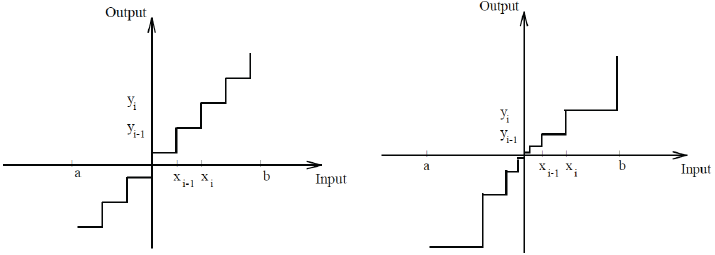
균일 양자화를 진행할때 어떤 수식을 통해 진행할것인가에 대한 내용이다. 마찬가지로 두가지 방식이 있는데, Affine Transfrom과 Scale Transform 방식이다. Affine Transform은 Asymmetric이라고도 하며 Scale Transform은 Symmetric 라고도 불린다.

 

 

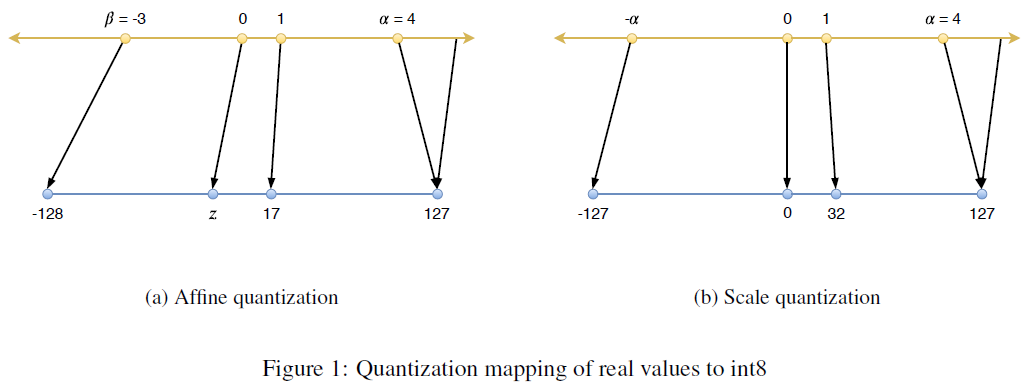
먼저 Affine Transform에 대해서 알아보자.

 

$$f\left(x\right)=s\cdot x+zs=\frac{2^b-1}{\alpha -\beta }z=-round(\beta \cdot s)-2^{b-1}$$

 

여기서 $\alpha ,\beta$는 입력값의 Min, Max를 의미한다. 모든범위에 대해서 Min, Max를 설정하면 적절하지 못하므로 Cutoff를 설정하고 Clip함수를 이용하여 잘라낸다. 위 그림의 (a)를 참고하면 알 수 있을것이다.

 

만약 8-Bit 양자화를 진행한다고 하면 Max값에 해당하는 $\alpha$가 127로, Min값에 해당하는 $\beta$는 -128로 scaling된다. $z$는 zero-point를 의미하는데, 변환되기 전 0의 위치가 양자화 후 어떤점으로 대응되는지 정확하게 표현하기 위함이다. 이렇게 함으로써 입력값의 분포를 고려한 양자화가 가능하다.

 

전체적인 수식을 살펴보면 아래와 같이 표현할 수 있다.

 

$$x_q=quantize(x,b,s,z)=clip\left(round\right(s\cdot x+z),-2^{b-1},2^{b-1}-1)$$

 

양자화된 값을 다시 원래값으로 복원 시키기기 위해서는 곱하고 더해준 방법을 거꾸로 진행한다. 즉, 빼고 나눠주면 된다. 양자화를 한 후 복원을 시키는 과정을 거치게되면 $\hat{x}\approx x$에 근사하게 된다는점을 기억해두자(추후 Fake_Quantization이란 용어를 사용한다).

 

$$\hat{x}=dequantize(x_q,s,z)=\frac{1}{s}(x_q-z)$$

 

이제 Scale Transform을 알아보도록 한다. Symmetric이라고 불린다고 하였는데, 그 이유는 입력값의 0이 양자화가 된 후 0의 값으로 정확히 대응되는 방법이기 때문이다(그림 (b)). 8-Bit로의 표현은 -128 ~ 127까지 표현가능하지만 대칭을 이뤄야하기 때문에 -128의 값은 사용하지 않는다. 또한 $\alpha$값으로 Max만을 사용한다.

 

$$f\left(x\right)=s\cdot xs=\frac{2^{b-1}-1}{\alpha }{x}_q=quantize(x,b,s)=clip\left(round\right(s\cdot x),-2^{b-1}+1,2^{b-1}-1)\hat{x}=dequantize(x_q,s)=\frac{1}{s}{x}_q$$

 

Quantization Granularity

어떤 세분화 단위에 입각하여 양자화를 진행할것인지에 관련한다. 예를들어 Tensor단위로 양자화 할것인지, 아니면 per Channel 단위로 양자화를 할것인지다. 저자는 정확도와 연산비용 두가지 측면을 고려해서 다음과 같이 제안하였다.

 

• weight: per-column(2D), per-channel(3D), per-tensor
• activation: per-tensor

 

활성화의 경우는 성능상 이유로 텐서단위 양자화가 실용적이라고 말하고 있다. 가중치의 경우에는 텐서단위 또는 채널단위 두가지를 모두 사용한다.

 

일반적인 신경망모델과 달리 비교적 EfficientNet의 경우에는 Depwise-Sperable Convolution 연산을 진행한다. 연산이 채널별로 각기 진행되기 때문에, per-channel 양자화를 진행해야하며 per-tensor 양자화를 진행하게되면 가중치의 분포가 흐트러지게 되어 성능이 더욱 나빠지게된다.

 

Computation Cost

우선 Scale Transform의 연산에 대해서 살펴보도록 하자.

 

$$y_{i,j}=\sum _{k=1}^p{x}_{ik}\cdot w_{kj}\approx \sum _{k=1}^{p}dequantize(x_{q,ik},s_{q,ik})\cdot dequantize(w_{q,kj},s_{w,kj})=\sum _k^p\frac{1}{s_{x,ik}}{x}_{q,ik}\cdot \frac{1}{s_{w,kj}}{w}_{q,kj}$$

 

맨 마지막 산식을 보면 아주 간단한 표현으로 나타나게 되있음을 알 수 있다. activation과 weight가 모두 양자화 되어있고 정수이기 때문에 빠르게 연산할 수 있음을 알 수 있다. $X_q$는 Offline에 계산될 수 없기 때문에 분명 연산상 오버헤드기는 하지만 내적 연산부분이 1개밖에 구성되어있지 않다.

 

이제 Affine Transform을 살펴보자.

 

$$y_{i,j}\approx \sum _{k=1}^p\frac{1}{s_x}(x_{q,ik}-z_x)\frac{1}{s_{w,j}}(w_{q,kj}-z_{w,j})=\frac{1}{s_x{s}_{w,j}}(\sum _k^p{x}_{q,ik}{w}_{q,kj}-\sum _k^p{w}_{q,kj}{z}_x+z_x{z}_{w,j}-\sum _k^p{x}_{q,ik}{z}_{w,j})$$

 

맨 마지막 산식을 보면 $X_q$가 한번 더 들어가있다. Offline에서 연산할 수 없는 텀이 두개나 들어가있다. 이는 Inference Time에 큰 오버헤드로 작용한다. 물론 Affine 방법이 정확도 측면에서는 좀더 우위를 차지할 수 있지만, 연산비용을 고려했을때 Scale 방법을 사용하는것이 더 좋다고 설명한다. 또 Scale 방법을 사용해도 정확도 손실이 엄청나게 큰것도 아니다.

 

Calibration

양자화를 진행할때 Scaling을 하기위한 $\alpha ,\beta$를 구하는것을 확인하였다. 앞에서는 Min, Max 방법을 이용한 예시를 들었으나, 사실 몇가지 방법이 더 존재한다.

 

 

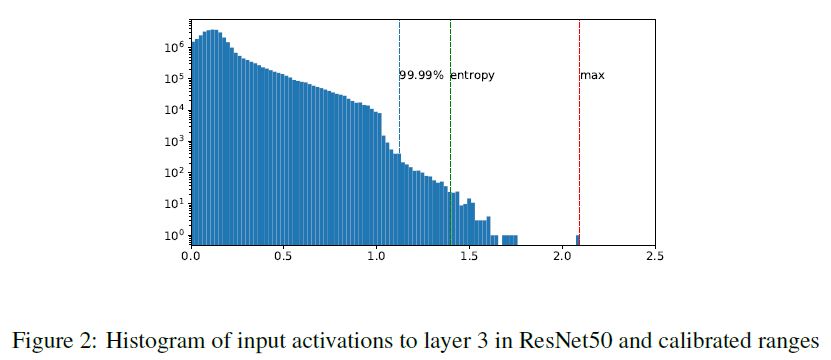
• Max: 원소값중 가장 큰 값의 절대값을 $\alpha$로 설정한다.
• Entropy: 양자화된 값과 기존 Floating-Point로 된 값의 차이가 최소가 되도록 $\alpha$를 설정한다. TensorRT 프레임워크에서는 Entropy가 디폴트이다.
• Percentile: 입력값의 분포를 백분위수로 나타내서 0.1%, 0.01% 등 사용자가 설정한 값에 해당하는 값을 $\alpha$로 설정한다.

 

Activation의 경우 Calibration을 진행하는것이 상당히 까다롭다. Input은 Offline에서 알 수 없는 변수상태라서 반드시 이미지가 들어온 후 Calibration이 진행되어야 한다. 또한 몇장의 이미지가 필요한지도 알 수 없다. 때문에 최대한 많은 샘플을 통해서 Calibration을 진행하는것이 효율적일것이며, 학습과 추론이미지의 분포를 최대한 유사할 수 있도록 이미지 획득을 하는것이 중요할 것이다.

 

Post-Training Quantizatio(PTQ)

이제 학습이 완료된 모델을 이용해서 양자화를 진행하는 PTQ의 결과에 대해서 알아볼 차례이다. 저자는 아래 그림과 같은 모델에 대해서 실험을 진행하였다.

 

 

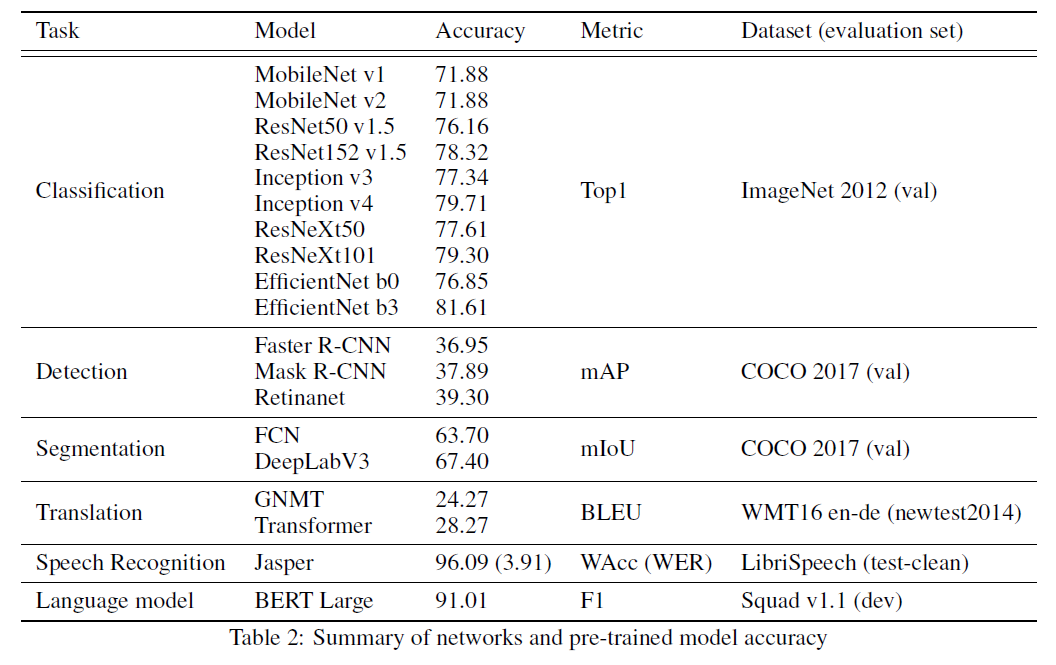
이미 학습이 완료되었기 때문에, Offline에서 가중이나 학습 파라미터들이 모두 설정되어있다는 특징이 있다. 때문에 Batch Norm Layer를 Bias처럼 취급하여 Conv Layer와 함께 Folding(Fusion이라고도 한다)하여 전체 Layer의 수를 줄일 수 있다.

 

 

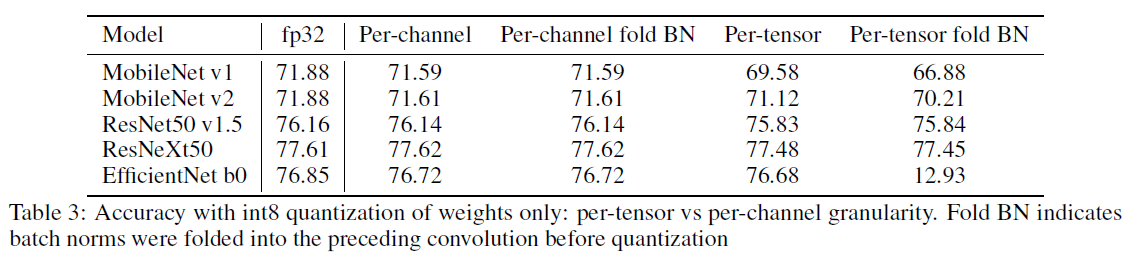
위에서도 설명했듯이 EfficientNet과 같은 특이한 형태의 Convolution을 하는 경우 Per-tensor의 사용을 조심하라고 설명했다. BN 또한 채널단위로 학습이 진행되기 때문에 무작정 Folding 하는것은 Weight의 분포를 박살내는것과 다름없다. 즉, 무작정 Folding을 하는것이 아니라 모델 아키텍쳐를 따져봐야한다는것을 알 수 있다.

 

Weight는 Per-Channel(또는 Per-Column)과 Max Calibration을 적용한 결과와 Activation에 대해서는 Per-Tensor와 다양한 Calibration을 적용했을때의 결과이다.

 

 

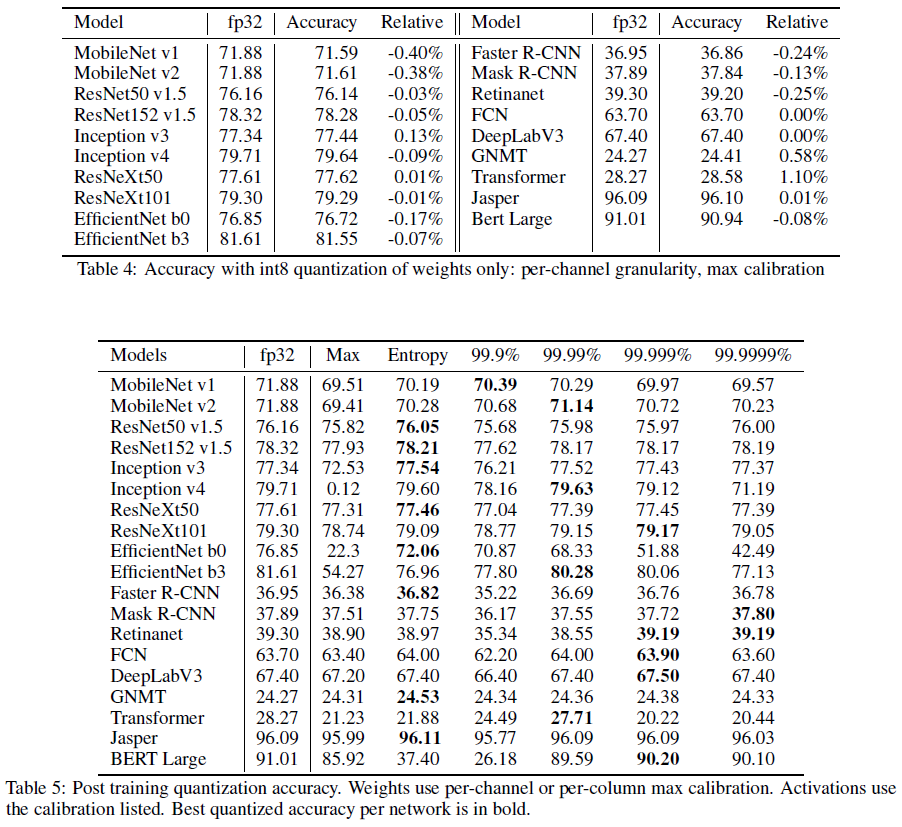
InceptionV4와 EfficientNet의 경우에는 Max Calibration을 적용했을때 결과가 매우 좋지 않다. 이는 활성화출력의 분포가 매우 극단적이라는것을 의미한다. 비교적 최신 모델이라고 불리는 모델에서 이러한 경향이 많이 나타나는데, 모델 아키텍쳐가 복잡해지기 때문이라 생각이 든다.

 

전체적인 경향성을 보았을때 Entropy 접근법이 가장 일반화적인 방법으로 보이며, TensorRT 프레임워크에서는 Entropy가 디폴트 Calibration 방법이다.

 

Partial Quantization

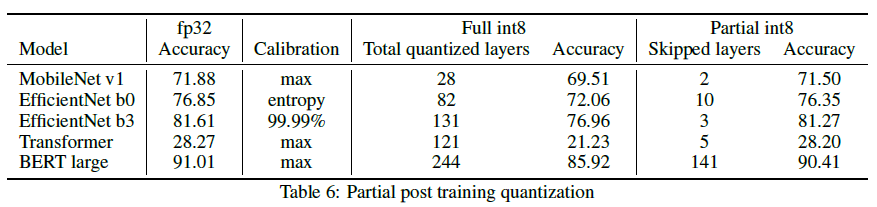
양자화를 진행하였을때 정확도 측면에서 좀더 개선할 수 있을 여지가 있다. 바로 Partial Quantization이다. 이 방법은 모든 Node를 양자화 진행하는것이 아니라, 마치 DropOut과 같이 몇개의 Node에서는 양자화를 진행하지 않는 방법이다.

 

 

신경망의 각 Layer를 Sensitive 기준으로 내림차순하여 하나씩 양자화를 죽여나가는 방법이다. 이때 Sensitive를 선정하는 기준은 안타깝게도 자세히 기재되어있지 않다. 어쨋든 이러한 방법으로 양자화를 단계적으로 진행을 하게되면 정확도를 보존할 수 있음을 보여준다.

 

 

Quantization-Aware Training(QAT)

학습이 진행되기 전 양자화를 진행하는 방법이다. 이전 포스팅에서 다루었던 Bi-RealNet, DoReFa-Net, XNOR-Net이 QAT에 해당한다. 일반적으로 QAT는 PTQ보다 성능이 우월하다. 이유는 아래 그림과 같다.

 

 

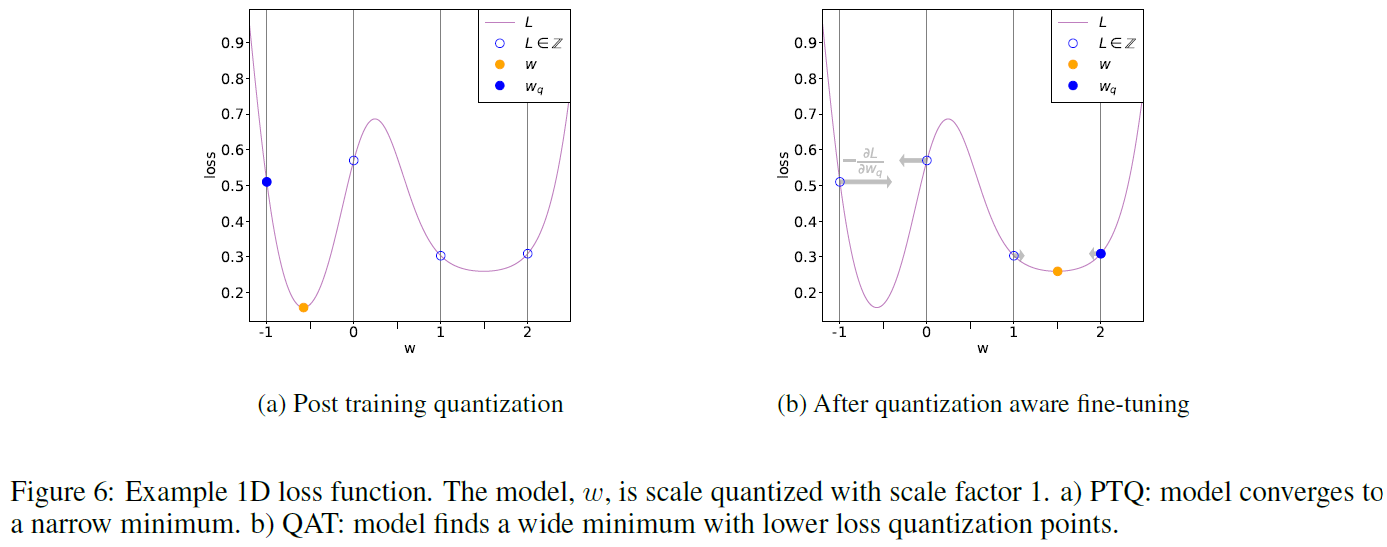
PTQ 방법은 이미 학습이 완료되어서 Global Minimun에 최적화되어있는 가중치를 덜 최적화된곳으로 보내버리게 된다. 이때 Loss가 Deep Convex인 경우에 문제가 발생한다. 가중치가 최적화된곳을 이탈하면서 Loss가 크게 상승하게된다(그림 6a).

 

하지만 QAT 방법은 이러한 문제를 방지한다. 학습을 진행하면서 최적화를 진행하기 때문에 가중치가 Deep Convex에 빠지기 어렵고, 오히려 narrow minima에 수렴하게 된다. 이 경우에 양자화가 진행되면 Loss의 형태가 Wide하기 때문에 PTQ 방식보다 성능이 더 좋게된다.

 

추가적으로 QAT 방식의 양자화는 앞서 얘기했던 Fake Quantization을 이용한다. Quantization을 진행하여 정수타입으로 변환 후 행렬연산을 진행하면 연산비용에서 상당히 이점을 가져올 수 있기 때문이다. 역전파가 불가능한 문제가 있기 때문에 STE 방법을 도입하며, 이것은 이전 포스팅에서 많이 다루었기 때문에 생략하고 넘어가겠다.

 

Recommended Workflow

저자가 여러 방법으로 실험을 한 이후 다음과 같은 양자화 방식을 제안한다.

 

 

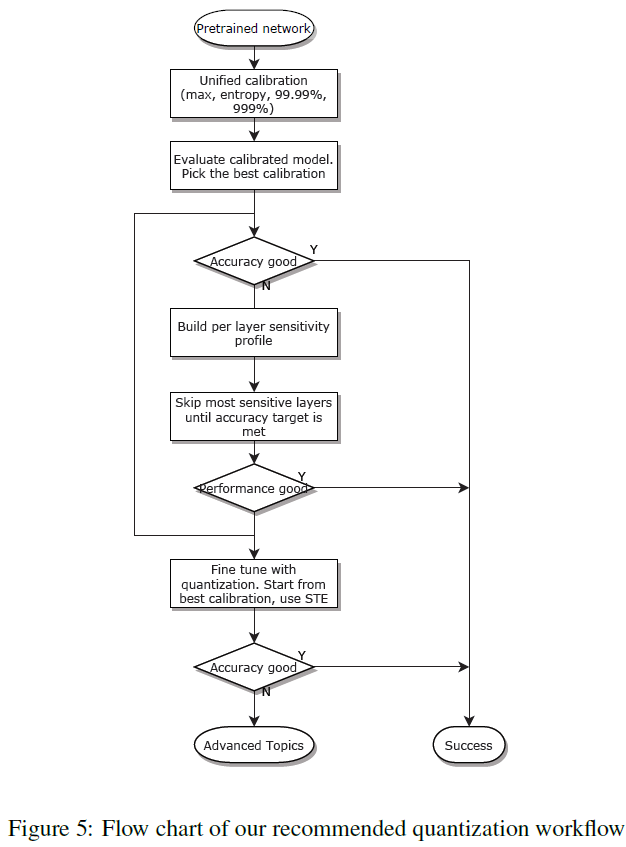
int8 양자화 방법으로는 아래와 같이 적용한다.

 

• weight: Scale Quantization 방식과 Per-Channel, Per-Column granularity를 적용한다. Calibration으로는 Max 방법을 사용한다.
• Activation: Scale Quantization 방식과 Per-Tensor granularity를 적용한다.

 

신경망을 양자화하기 위한 과정으로는 아래와 같은 순서로 적용해 나간다.

 

• PTQ: PTQ 방법을 우선적으로 고려한다. 앞서 학습했던 Max, Entropy, Percentile Calibration에 대해서 다양하게 적용해가며 성능을 확인한다.
• Partial Quantization: PTQ 방법이 조금 아쉬울때 적용해본다. Sensitive 기준으로 내림차순하여 하나씩 양자화를 죽여나가며 성능을 확인한다.
• QAT: 위 두가지 방법으로도 성능이 개선되지 않을때 사용한다.

 

Conclusions

양자화의 기본개념에 대해서 아주 상세히 설명해주어서 나와같은 입문자에게 엄청 도움이 되었다. 영어단어 선택이나 문장구성이 비교적 읽기 편하게 되어있어서 이해가 쉬웠고, 특히 Pytorch로 실험이 이루어져있어서 추후 적용하는것도 손쉬울것 같았다. 양자화 적용을 한번 도전했다가 실패했던 경험이 있었는데, 이 내용을 토대로 다시한번 도전을 해 보아야겠다.